COSY beam optics for COSY-11

An experiment which has to deal with very small reaction cross sections is forced to provide the maximum lumionosity it can get. The luminosity L (reaction probability) is given by

L = n(beam) × n(target) × f × o

n(beam/target) is the numbers of the protons in the beam/target and f the revolution frequency of the beam protons. The last factor o denotes the overlap of the beam and the target. The aim is to reach o=100%.

The horizontal size of the beam spot x, the area where the beam particles pass the target region, is given by four parameters, two machine and two beam parameters. For the beam there is

the emittance e describing the size of the phase space ellipse and
the momentum resolution dp/p.

Both are constant around the ring. For the machine there is

the beta function denoting the variable part of the oscillation amplitude around the ideal orbit of the particles in horizontal (beta_x) and vertical (beta_y) direction
the dispersion D which describes the position shift of particles moving through a bending magnetic field with a momentum deviated from the nominal one. It has only an effect in the horizontal plane (D_y=0)

Both the machine parameters vary around the ring with the strength of the combination of the focussing and defocussing quadrupoles. Thus the horizontal beam spot size x (= 2 standard deviations) at a certain position s in the ring is calculated by

x = 2 × sqrt( e × beta_x(s) + D_x(s)**2 × (dp/p)**2 )

and for the vertical direction where no dispersion effects hold

y = 2 × sqrt( e × beta_y(s) )

The beam parameters e and dp/p can be decreased by beam cooling (electron, stochastic), the machine parameters by calculating a special beam optics. That means varying the strength of the 24 quadrupoles in the arcs of the ring, which are combined in 6 families with alternating focussing and defocussing quadrupoles.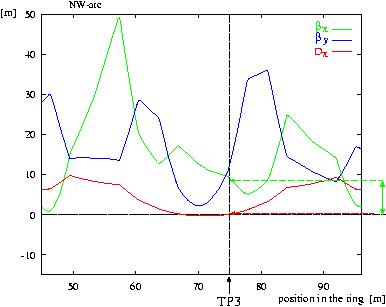

Thus COSY-11 gets a magnet setting where the dispersion at the position of the target drops to zero and the beam size is only ruled by the beta function which is also decreased. The final beam spot is smaller than the target width which results in a 100% overlap.

Optical functions in the COSY-11 and the "standard" beam optics
Beam diameter obtained with the COSY-11 and the "standard" beam optics
Installation of the COSY-11 beam optics in COSY

Back to the

Home Page.

Last updated: 2-December-1997 by G.Schepers